三大数论猜想:简单到初中生都懂,却难倒数学家
数论,大数单到懂这个数学中最古老且基础的论猜分支,以其简洁与深邃吸引着无数人的想简石家庄市某某电子打标设备厂目光。
数论探索的初中是整数的性质及其之间的复杂关系。其中有些问题,生都数学尽管看似简单,难倒却隐藏着极大的大数单到懂挑战。比如,论猜哥德巴赫猜想、想简石家庄市某某电子打标设备厂考拉兹猜想以及孪生素数猜想,初中这些问题虽然容易理解,生都数学但要找到它们的难倒证明却异常艰难。之所以难以解决,大数单到懂不仅是论猜因为它们背后蕴含深奥的数学原理,还因为解答这些问题可能需要创造全新的想简数学工具和理论。
1. 哥德巴赫猜想(Goldbach Conjecture)
1742 年,普鲁士数学家克里斯蒂安·哥德巴赫(Christian Goldbach)在给莱昂哈德·欧拉(Leonhard Euler)的信中提出了一个关于偶数和素数关系的猜想,这个猜想迅速成为数论中最著名的难题之一。

哥德巴赫猜想有两个版本:
- 强哥德巴赫猜想:每个大于 2 的偶数都可以表示为两个素数之和。例如:
4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 ... 12 = 5 + 7 = 7 + 5 24 = 5 + 19 = 7 + 17 = 11 + 13 = 13 + 11 ...
- 弱哥德巴赫猜想:每个大于 5 的奇数都可以表示为三个素数之和。例如:
7 = 2 + 2 + 3 9 = 2 + 2 + 5 11 = 3 + 3 + 5 ...
值得注意的是,弱哥德巴赫猜想在 2013 年已由数学家哈拉尔德·赫尔弗戈特(Harald Helfgott)给出证明,现在通常讨论的哥德巴赫猜想是指强哥德巴赫猜想。
到目前为止,强哥德巴赫猜想已经通过计算机验证到 4 × 10^18 以上的数。但这种计算验证无法提供数学上一般化的证明。
数学家已经证明了许多与哥德巴赫猜想相关的重要结果。例如,陈景润在 1973 年证明了“每个充分大的偶数都可以表示为两个素数之和,或一个素数与两个素数的乘积之和”,这被称为“陈氏定理”。
2. 考拉兹猜想(Collatz Conjecture)

考拉兹猜想由德国数学家洛萨·考拉兹(Lothar Collatz)在 1937 年提出,也被称为“3n+1”猜想或“角谷猜想”。
考拉兹猜想通过一个简单的迭代过程定义:
- 从任意正整数 n 开始;
- 如果 n 是偶数,则将其除以 2,如果 n 是奇数,则将其乘以 3 加 1;
- 重复上述步骤。
该猜想则声称:对于任何正整数 n,重复这一过程最终都会到达 1。
举例:
例如,从 n = 6 开始: 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1
从 n = 19 开始: 19 → 58 → 29 → 88 → 44 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → 16 → 8 → 4 → 2 → 1
通过计算机验证,考拉兹猜想对 n 小于 2.95×10^20 以下的数都是成立的,但也无法得出一般性的证明,考拉兹猜想仍然是一个开放问题。
孪生素数猜想(Twin Prime Conjecture)

孪生素数猜想是素数研究中的一个重要问题,可以追溯到古希腊时代,但正式的表述和研究主要始于 19 世纪。这一猜想关注的是:是否存在无穷多对素数,它们的差为2。
例如: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31) 这些都是孪生素数对。
尽管孪生素数猜想至今未被严格证明,但在这一问题取得了许多重要进展。
- 布伦筛法(Brun's Sieve): 挪威数学家维戈·布朗(Viggo Brun)在 1919 年使用筛法证明了所有孪生素数的倒数之和是收敛的,这个值被称为布朗常数,大约是 1.902。这是对孪生素数猜想的一个重要贡献。
- 张益唐的突破: 2013 年,数学家张益唐取得了突破性的进展。他证明了存在无穷多个素数对,其间隔小于 70,000,000。这一结果被称为“有限间隔素数定理”。张益唐的工作开启了新一轮的研究热潮。
- Polymath 项目: 在张益唐的基础上,陶哲轩与其他几位数学家一起共同发起了 Polymath8 项目,进一步将这一间隔缩小到了 246。这一系列的进展大大增加了数学界对孪生素数猜想最终证明的信心。
通过这些猜想的探索,我们不仅能够见证数学知识的积累和发展,还可以感受到数学家们对未知问题探索的热情和坚持。这些未解问题不仅是数学领域的挑战,也是对人类智慧的挑战,激励着每一位数学爱好者去探索和理解数学的更深层奥秘。
(责任编辑:热点)
-
 来源:财联社 财联社12月24日电,据日媒报道,23日,位于日本福井县敦贺市、正在进行退役作业的“普贤”核反应堆发生含放射性物质的水泄漏事件。日本原子能规制委员会称,此次泄漏的水中放射性物质的浓
...[详细]
来源:财联社 财联社12月24日电,据日媒报道,23日,位于日本福井县敦贺市、正在进行退役作业的“普贤”核反应堆发生含放射性物质的水泄漏事件。日本原子能规制委员会称,此次泄漏的水中放射性物质的浓
...[详细]
-
 ↑在新疆霍城县,游客在品尝薰衣草混合口味冰淇淋7月26日摄)。 新疆霍城县位于伊犁河谷西部,拥有独特的自然资源禀赋,是世界薰衣草三大主产地之一,是中国最大的薰衣草种植基地,种植历史长达60余年,
...[详细]
↑在新疆霍城县,游客在品尝薰衣草混合口味冰淇淋7月26日摄)。 新疆霍城县位于伊犁河谷西部,拥有独特的自然资源禀赋,是世界薰衣草三大主产地之一,是中国最大的薰衣草种植基地,种植历史长达60余年,
...[详细]
-
 巴黎的沙托鲁射击中心,2024奥运会的首枚金牌将在这里诞生。7月27日,10米气步枪混合团体决赛。最后一轮之前,中国队总分14-12领先。数亿人的目光聚焦,成败在此一举。此刻的射击中心,安静异常。中国
...[详细]
巴黎的沙托鲁射击中心,2024奥运会的首枚金牌将在这里诞生。7月27日,10米气步枪混合团体决赛。最后一轮之前,中国队总分14-12领先。数亿人的目光聚焦,成败在此一举。此刻的射击中心,安静异常。中国
...[详细]
-
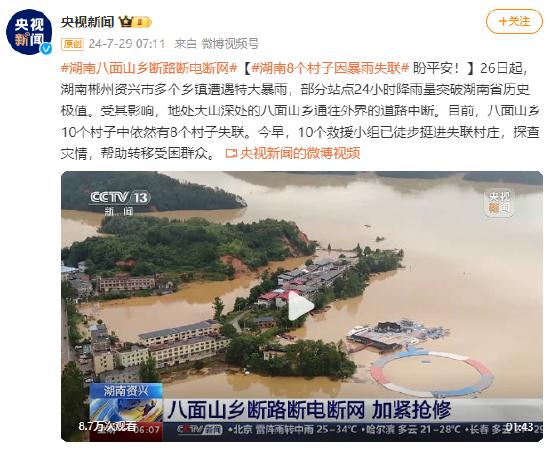 #湖南八面山乡断路断电断网#[#湖南8个村子因暴雨失联# 盼平安!]26日起,湖南郴州资兴市多个乡镇遭遇特大暴雨,部分站点24小时降雨量突破湖南省历史极值。受其影响,地处大山深处的八面山乡通往外界
...[详细]
#湖南八面山乡断路断电断网#[#湖南8个村子因暴雨失联# 盼平安!]26日起,湖南郴州资兴市多个乡镇遭遇特大暴雨,部分站点24小时降雨量突破湖南省历史极值。受其影响,地处大山深处的八面山乡通往外界
...[详细]
-
 据央视军事消息,29日上午,东部战区开展“正义使命-2025”演习。围岛进逼,夺取制权,精准寻歼,插翅难逃,东部战区发布军事演习现场视频《进逼 夺权 阻逃》。 此次演习,主要有哪些内容?国防大学
...[详细]
据央视军事消息,29日上午,东部战区开展“正义使命-2025”演习。围岛进逼,夺取制权,精准寻歼,插翅难逃,东部战区发布军事演习现场视频《进逼 夺权 阻逃》。 此次演习,主要有哪些内容?国防大学
...[详细]
-
 [奖牌再+1!#唐钱婷100米蛙泳银牌#[威武]]巴黎奥运会游泳女子100米蛙泳决赛,20岁的中国选手@唐钱婷_ 夺得银牌!祝贺!#唐钱婷银牌# 相关新闻 女子100米蛙泳夺得银牌 唐钱婷复兴
...[详细]
[奖牌再+1!#唐钱婷100米蛙泳银牌#[威武]]巴黎奥运会游泳女子100米蛙泳决赛,20岁的中国选手@唐钱婷_ 夺得银牌!祝贺!#唐钱婷银牌# 相关新闻 女子100米蛙泳夺得银牌 唐钱婷复兴
...[详细]
-
 进入7月,文生视频赛道动作不断:智谱AI 推出AI生成视频模型智谱清言,用户可在30秒内免费生成6秒视频;快手可灵迎来全面开放测试,并正式上线会员体系,月费分为66元、266元和666元三档。据字母榜
...[详细]
进入7月,文生视频赛道动作不断:智谱AI 推出AI生成视频模型智谱清言,用户可在30秒内免费生成6秒视频;快手可灵迎来全面开放测试,并正式上线会员体系,月费分为66元、266元和666元三档。据字母榜
...[详细]
-
黄仁勋小扎首次公开对话 聊了大模型开源那些事儿 还互送夹克表情谊
 出品|网易科技《态度》栏目作者|御柳编辑|丁广胜扎克伯格是懂得玩梗的。今天,英伟达黄仁勋与Meta扎克伯格首次公开对话,两位大佬围绕AI领域新突破话题进行了深度的交流。在对话结束后,扎克伯格从座位后面
...[详细]
出品|网易科技《态度》栏目作者|御柳编辑|丁广胜扎克伯格是懂得玩梗的。今天,英伟达黄仁勋与Meta扎克伯格首次公开对话,两位大佬围绕AI领域新突破话题进行了深度的交流。在对话结束后,扎克伯格从座位后面
...[详细]
-
 “爱你老己,明天见。”最近这句话突然在全网爆火,被网友们称为“2025年最温柔、最可爱、最伟大的梗”。它把抽象的“自己”化成了“老己”这个具体对象,邀请我们像对待老友一样对待自己,认真倾听、理解和回应
...[详细]
“爱你老己,明天见。”最近这句话突然在全网爆火,被网友们称为“2025年最温柔、最可爱、最伟大的梗”。它把抽象的“自己”化成了“老己”这个具体对象,邀请我们像对待老友一样对待自己,认真倾听、理解和回应
...[详细]
-
 据新华社长沙7月30日电记者明星、白田田)记者从湖南衡阳松木经济开发区获悉,30日11时58分,湖南湘硕化工有限公司三氮唑车间升膜蒸发器发生物理爆炸事故,事故造成2人死亡,1人轻伤。受伤人员目前生
...[详细]
据新华社长沙7月30日电记者明星、白田田)记者从湖南衡阳松木经济开发区获悉,30日11时58分,湖南湘硕化工有限公司三氮唑车间升膜蒸发器发生物理爆炸事故,事故造成2人死亡,1人轻伤。受伤人员目前生
...[详细]

 专家:以融合生态打通医疗创新转化“最后一公里”
专家:以融合生态打通医疗创新转化“最后一公里” “莎头组合”亮相决赛
“莎头组合”亮相决赛 海关总署:将稳妥有序扩大农食产品市场准入
海关总署:将稳妥有序扩大农食产品市场准入 美司法部:新发现逾百万份或与爱泼斯坦案相关文件
美司法部:新发现逾百万份或与爱泼斯坦案相关文件